Sudoku, the captivating number puzzle, has been a favorite for ages. But have you ever wondered what’s happening behind the scenes in the apps and websites that can solve any Sudoku in a flash? The secret often lies in an elegant algorithm known as backtracking.

In this post, we’ll explore the backtracking algorithm, uncovering how it’s used not only to solve Sudoku puzzles but also to create new ones with unique solutions.

What is Backtracking?

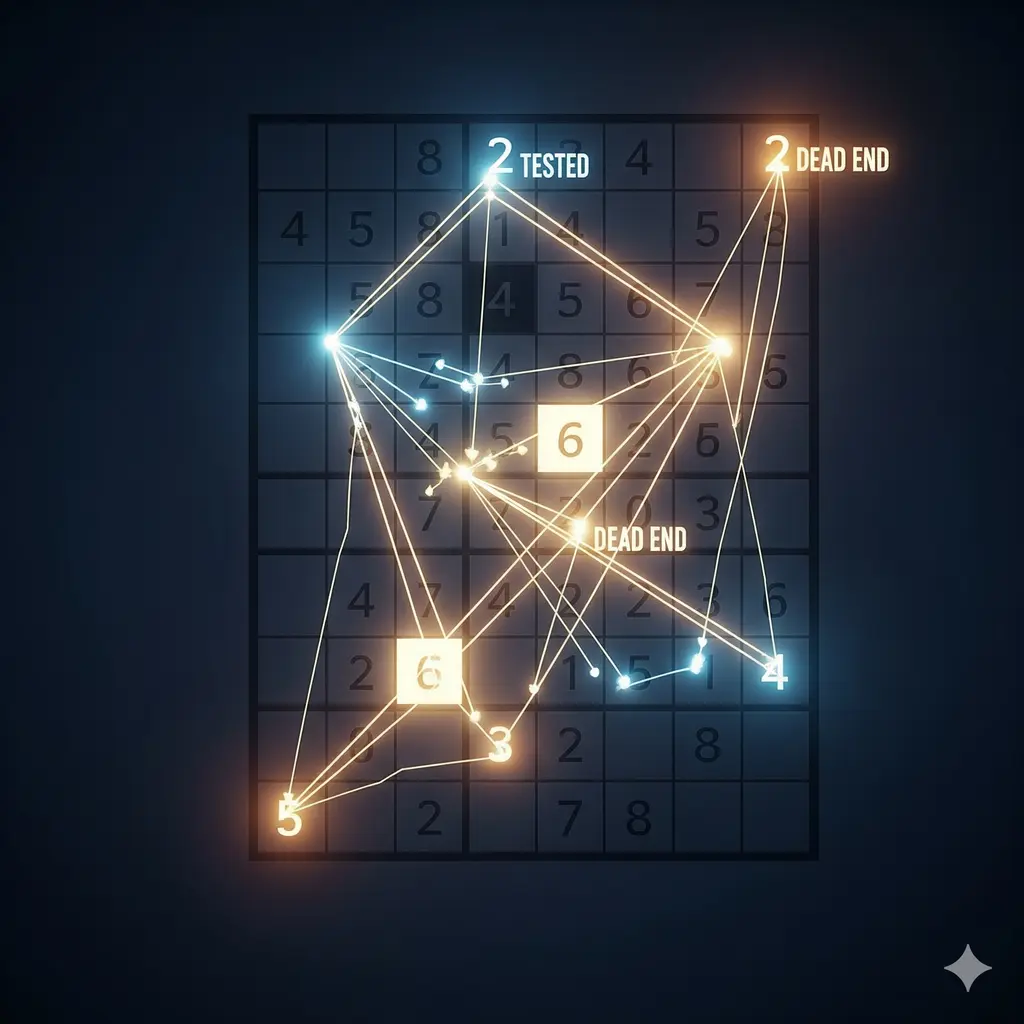
At its core, backtracking is a methodical trial-and-error technique. It’s all about making a choice, and if that choice doesn’t lead to a solution, you go back and try a different one.

Think of it like navigating a maze. You follow one path, and if you hit a dead end, you “backtrack” to the last junction and try a different route. You repeat this process until you find your way out.

Solving Sudoku with Backtracking

In the world of Sudoku, the “maze” is the grid, and the “paths” are the possible numbers (1-9) you can place in each empty cell. Here’s how the algorithm works:

1. Find an Empty Cell: First, it scans the grid to find an empty cell. If there are no empty cells, the puzzle is solved!
2. Try Numbers 1-9: For that empty cell, it tries placing a number, starting from 1.
3. Check for Validity: For each number, it checks if the move is valid according to Sudoku rules:
   • The number can’t already be in the same row.
   • The number can’t already be in the same column.
   • The number can’t already be in the same 3x3 subgrid.
4. Move On: If the number is valid, the solver calls itself to tackle the next empty cell. This process repeats, diving deeper into the puzzle.
5. Backtrack: If the solver gets stuck (meaning, it hits a dead end), it means the number it last placed was incorrect. So, it “backtracks” by resetting the cell to empty and trying the next number in the sequence.

If all numbers from 1 to 9 have been tried and none work, the function returns, and the previous step takes over, trying a new number in the cell before it.

Generating Sudoku Puzzles

Generating a Sudoku puzzle is just as interesting and also relies on the backtracking solver. The main goal is to create a puzzle that has only one possible solution.

1. Start with a Solved Grid: First, the algorithm generates a completely solved Sudoku grid. This is done by applying the backtracking solver to an empty grid.

2. Remove Numbers: With a solved grid, it then starts removing numbers one by one from random cells.

3. Check for a Unique Solution: After each number is removed, it needs to be sure that the puzzle still has only one unique solution. This is where the backtracking algorithm comes in handy once more. A modified version of the solver is used to count the number of possible solutions.

4. Undo if Necessary: If removing a number results in a puzzle with more than one solution (or no solution), the removal is undone (the number is put back), and the algorithm tries removing a different number.

This continues until enough cells have been removed to create a challenging but fair Sudoku puzzle.

Conclusion

The backtracking algorithm is a powerful yet intuitive tool that elegantly handles the complexities of Sudoku. Its trial-and-error approach is perfect for solving these puzzles and is cleverly repurposed for generating them. So, the next time you’re enjoying a Sudoku, you can appreciate the simple and profound logic that can unravel even the most challenging grids.